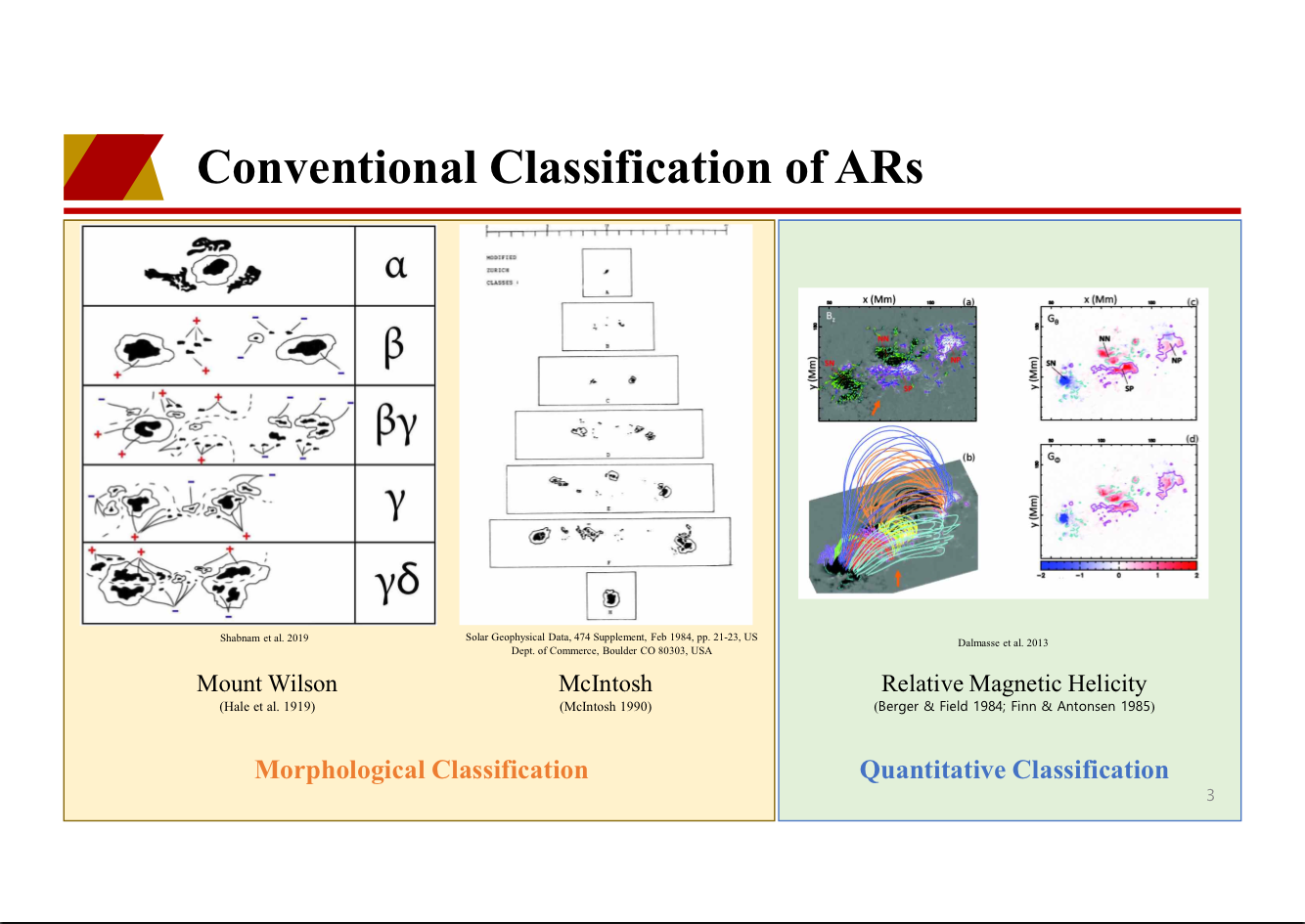
Quantitative characterization of active-region magnetic structure based on geometric
property of force-free α
We investigated the geometric property of force-free
α (scalar position function) to see how it may quantitatively characterize magnetic structure of solar active
region (AR), as seen in the case of electrostatic potential (scalar position function) whose geometric property
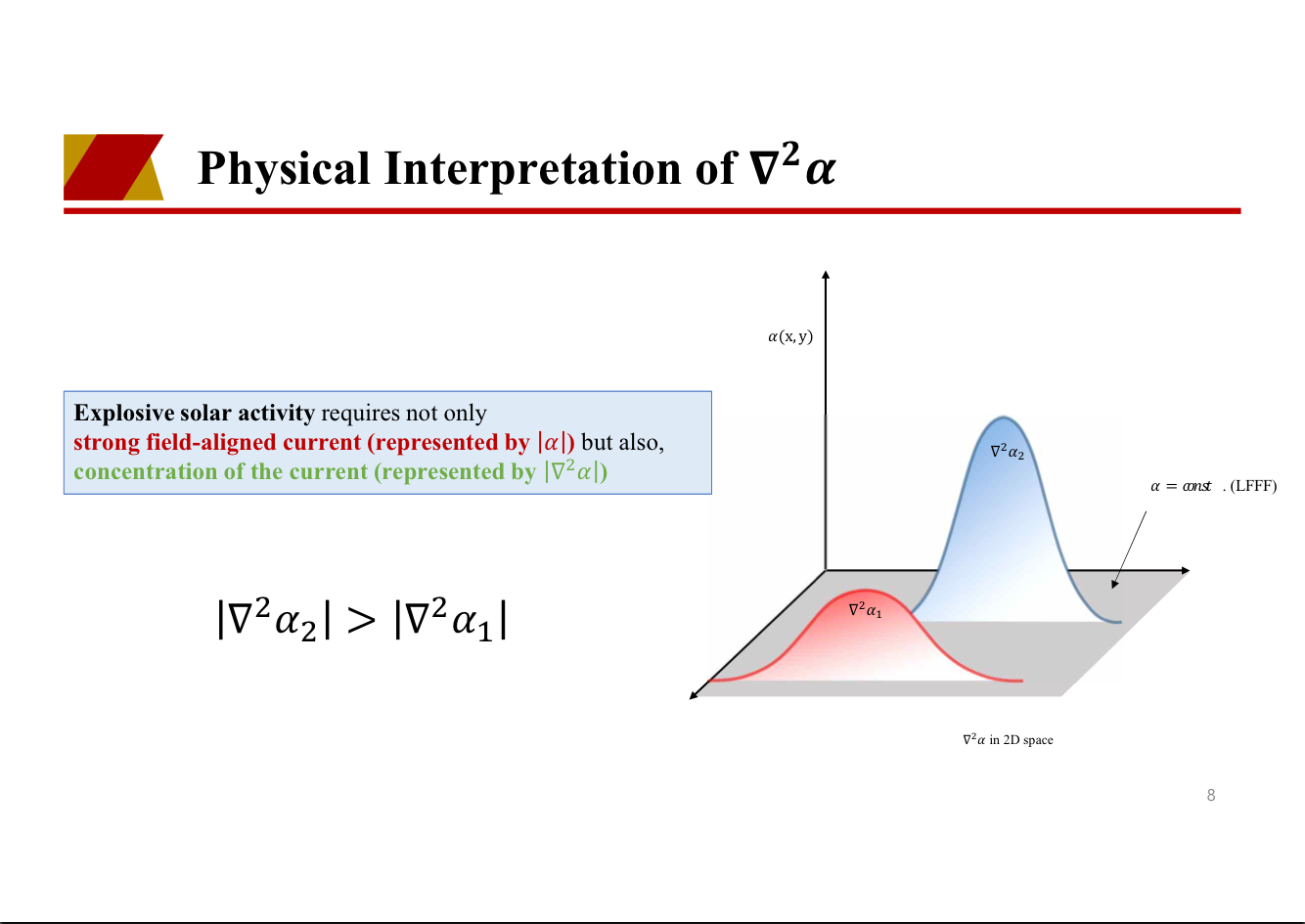
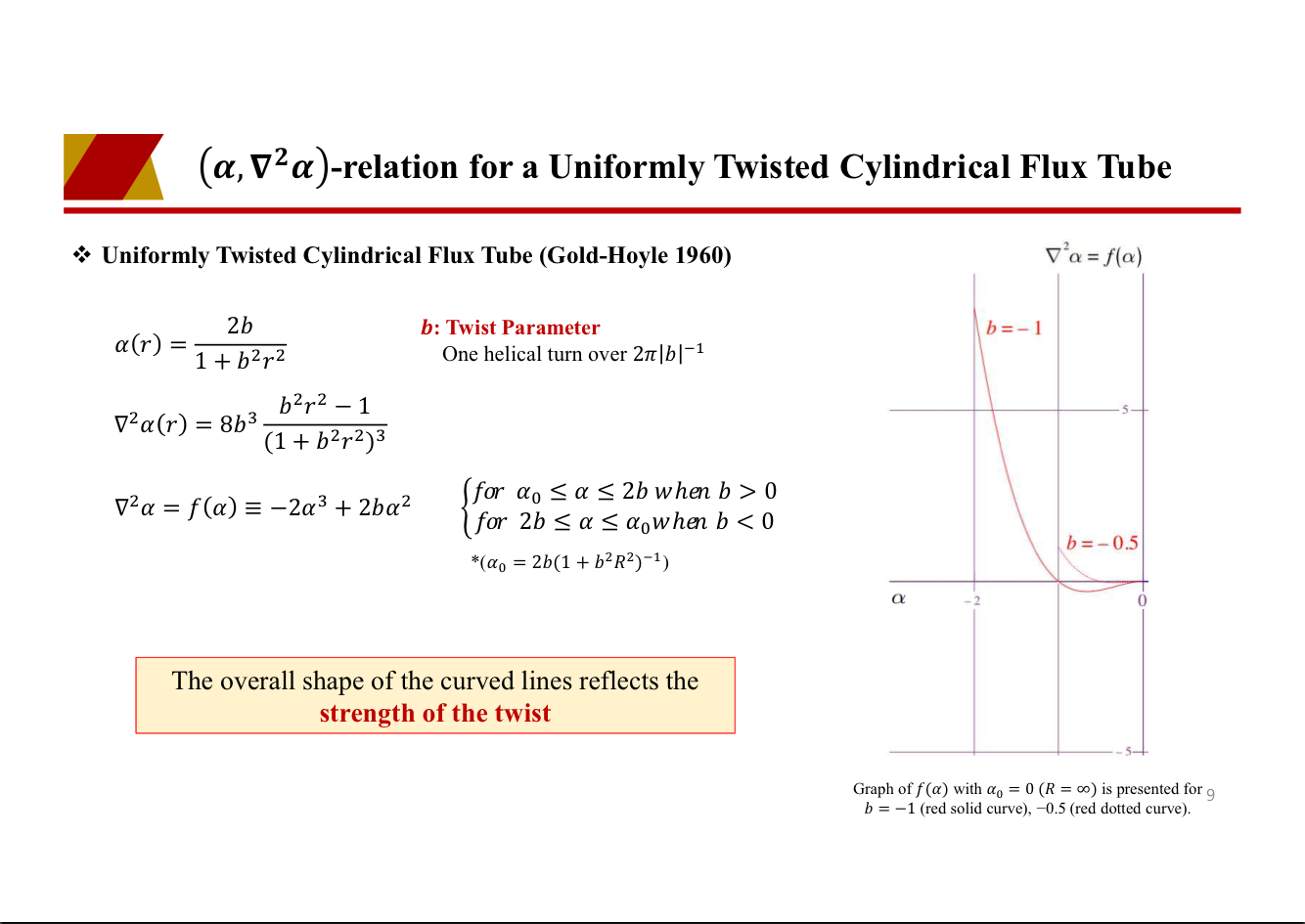
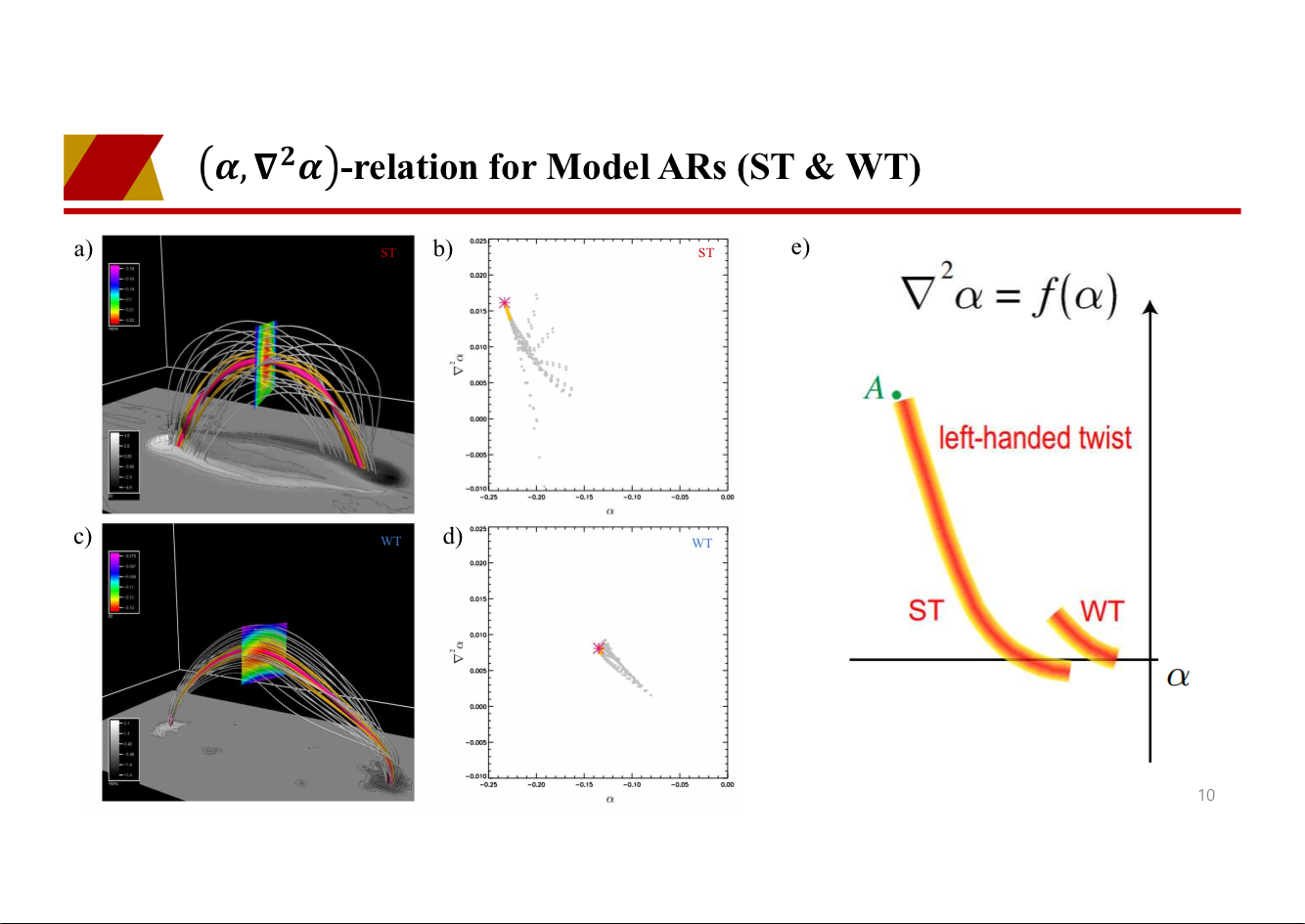
provides quantitative information on structure of electrified object. The geometric property of force-free α was quantitatively expressed using the relation between α and ∇2α, and we derived scatter plots of (α, ∇2α) in two modeled ARs, one of which was produced by an emerging magnetic flux tube composed of strongly twisted field lines, while the other weakly twisted field lines. These scatter plots showed a characteristic shape depending on strength of field-line twist and its spatial concentration. By generalizing the concept of an axis field line in a uniformly twisted cylindrical flux tube,
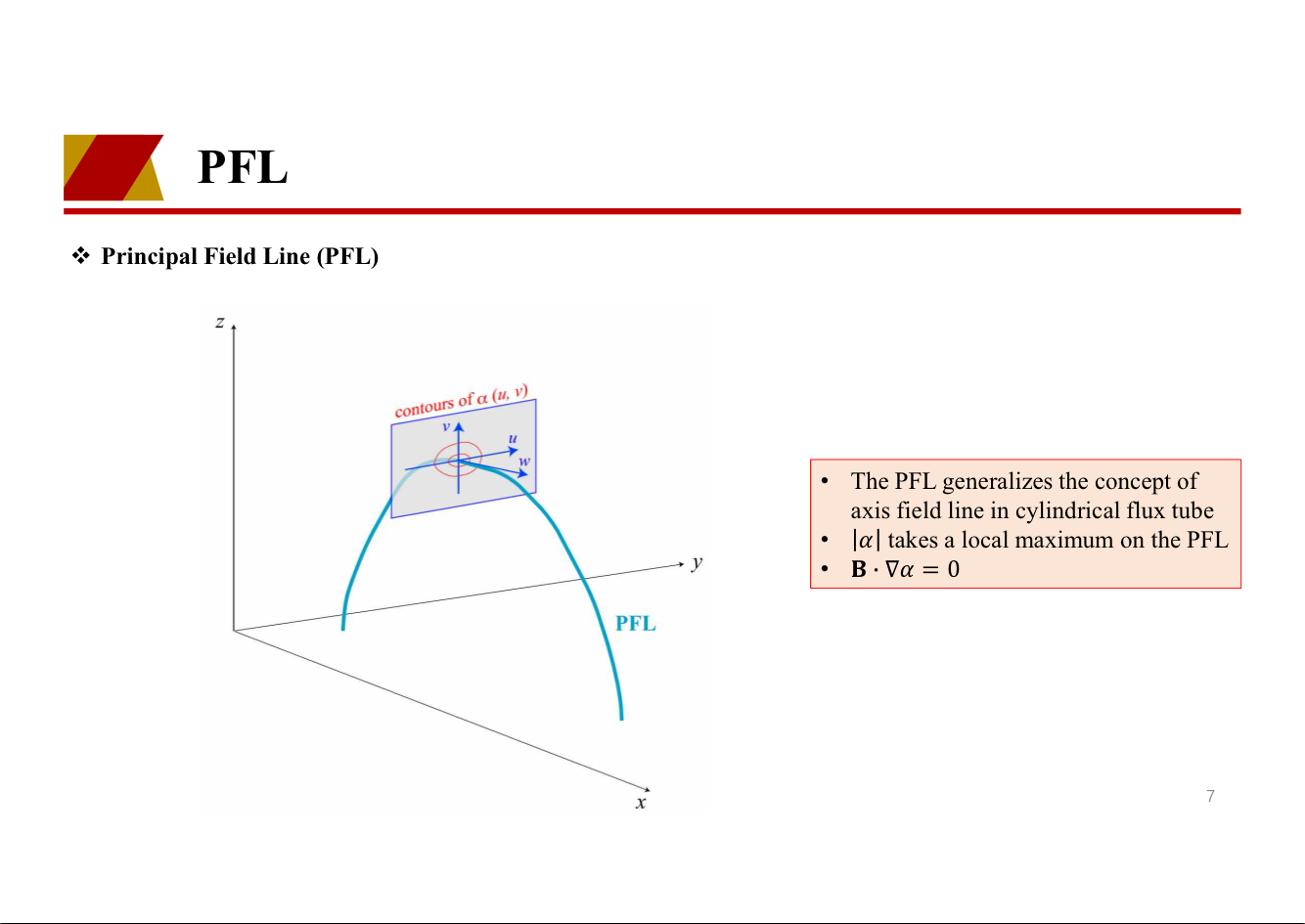
we introduced a topological object called principal field line (PFL) that is determined from the (α, ∇2α)-relation to represent magnetic structure reconstructed with a nonlinear force-free field model. PFL and the associated scatter plot of (α, ∇2α) may provide a method reminiscent of AR radiography (ARR), in which AR’s bones are displayed as a set of PFLs and each bone (= PFL) is
colored using quantitative information derived
from the scatter plot.
The method could be used for a quantitative classification of ARs with those magnetic field
configurations responsible for heating coronal plasmas, generating solar winds,
and producing potentially harmful coronal explosive phenomena.
Reference
Jang, Y., Yi. S., and Magara, T. 2023, PASJ, 75, 787
Appendix I. Comparison to electrostatic potential
A comparison between graphs of force-free α [∇2α = f(α)] and electrostatic potential φc [∇2φc = g(φc)]
suggests that certain types of force-free magnetic structure
and electrostatic structure are characterized using these
graphs in a similar way. A common feature of them is
that the graph of f(α) [g(φc)] has a characteristic shape
when a field-line twist [charge] exists; that is, the shape
reflects the handedness and strength of the twist [polarity
and concentration of the charge].
Appendix II. (α, ∇2α)-relation for 2.5D force-free magnetic structure
