Inversion method for deriving physical properties of subsurface magnetic field from surface magnetic field evolution.
II. Application to Observed Data
This work is intended to demonstrate how to apply an inversion method to one of the observed solar active regions (ARs) generally having complex magnetic structure. The method was developed in our previous work for solving an inverse problem to derive physical properties of a subsurface magnetic field from observed evolution of a surface magnetic field. We handled two key issues in the application of the method to the observed AR (AR10930), one of which is to reconstruct three-dimensional magnetic structure of the AR, while the other is to select a single magnetic flux tube responsible for an X-class flare observed in this AR by isolating closed magnetic-loop structure from the reconstructed AR structure. The isolation of the loop structure is essential for a proper evaluation of unsigned magnetic flux and relative magnetic helicity, both of which are used to solve the inverse problem via curve-fitting analysis.
By refining data of the so-called force-free α, we derived the principal field line representing the axis of the selected flux tube in the AR, which could contribute to a quantitative classification of ARs having full of variety in size, magnetic field strength, and magnetic field configuration.
Reference
Magara, T., Yi, S., Jang, Y., & Son, D.
Journal of the Korean Astronomical Society, 58, 305

AR10930 consists of two major sunspots, one of which has negative magnetic polarity and larger size than the other, i.e., positive sunspot. The X-class flare occurred above a local polarity inversion line between these two sunspots.
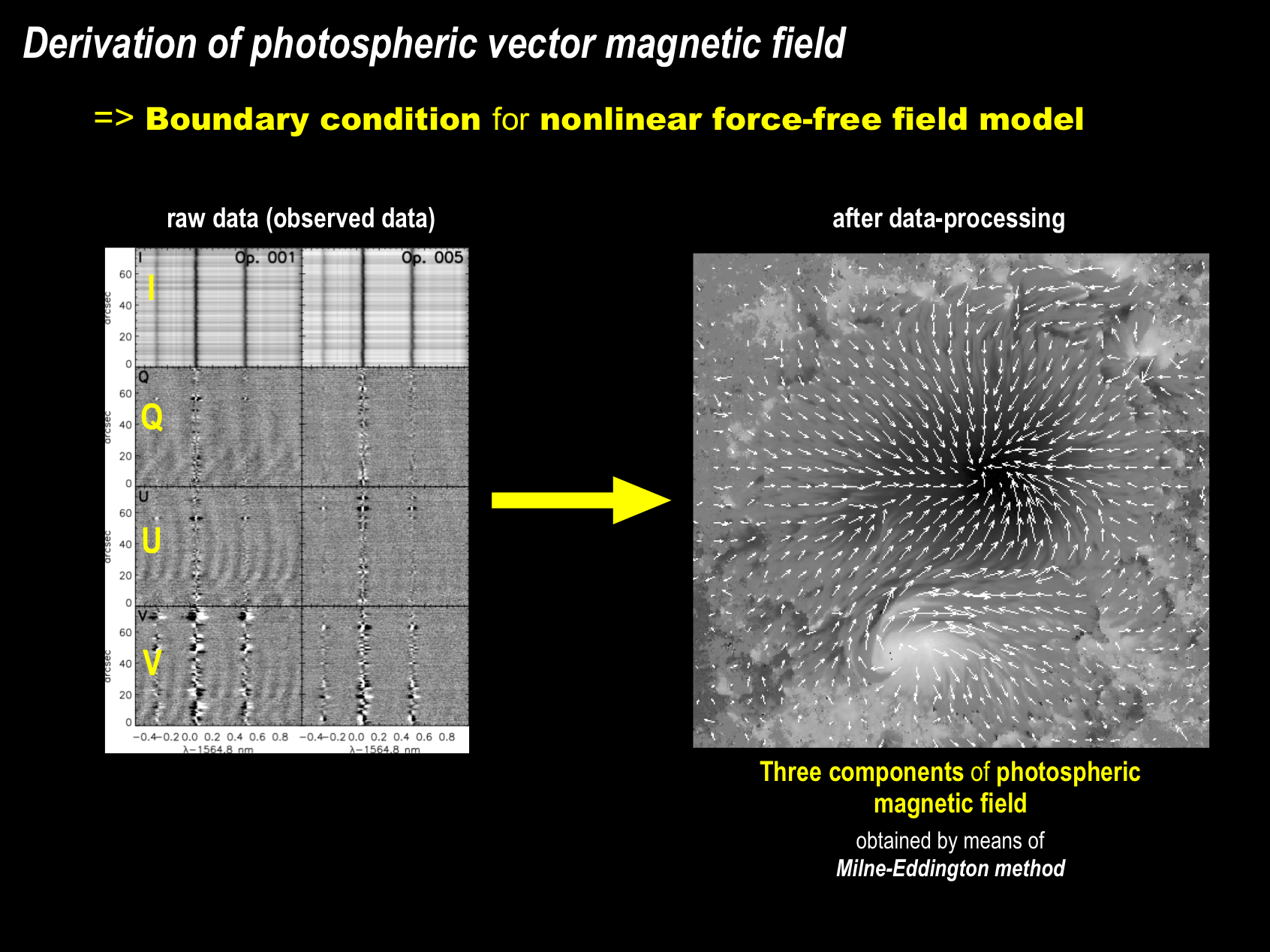
The observed data of AR 10930 used for the present work comprises three components of magnetic field distributed in the photosphere.
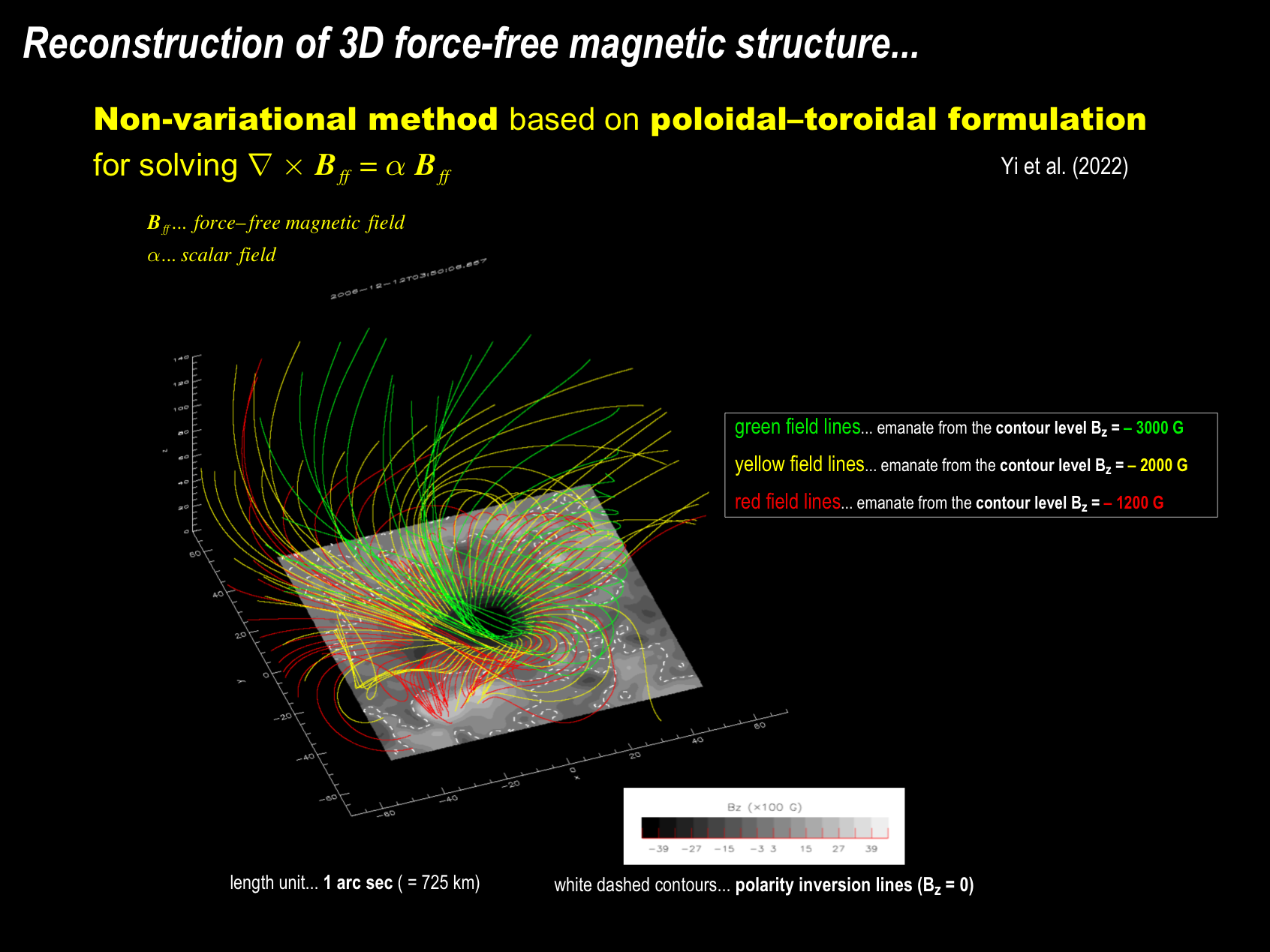
The photospheric field data was used to derive a nonlinear force-free field (Bff).
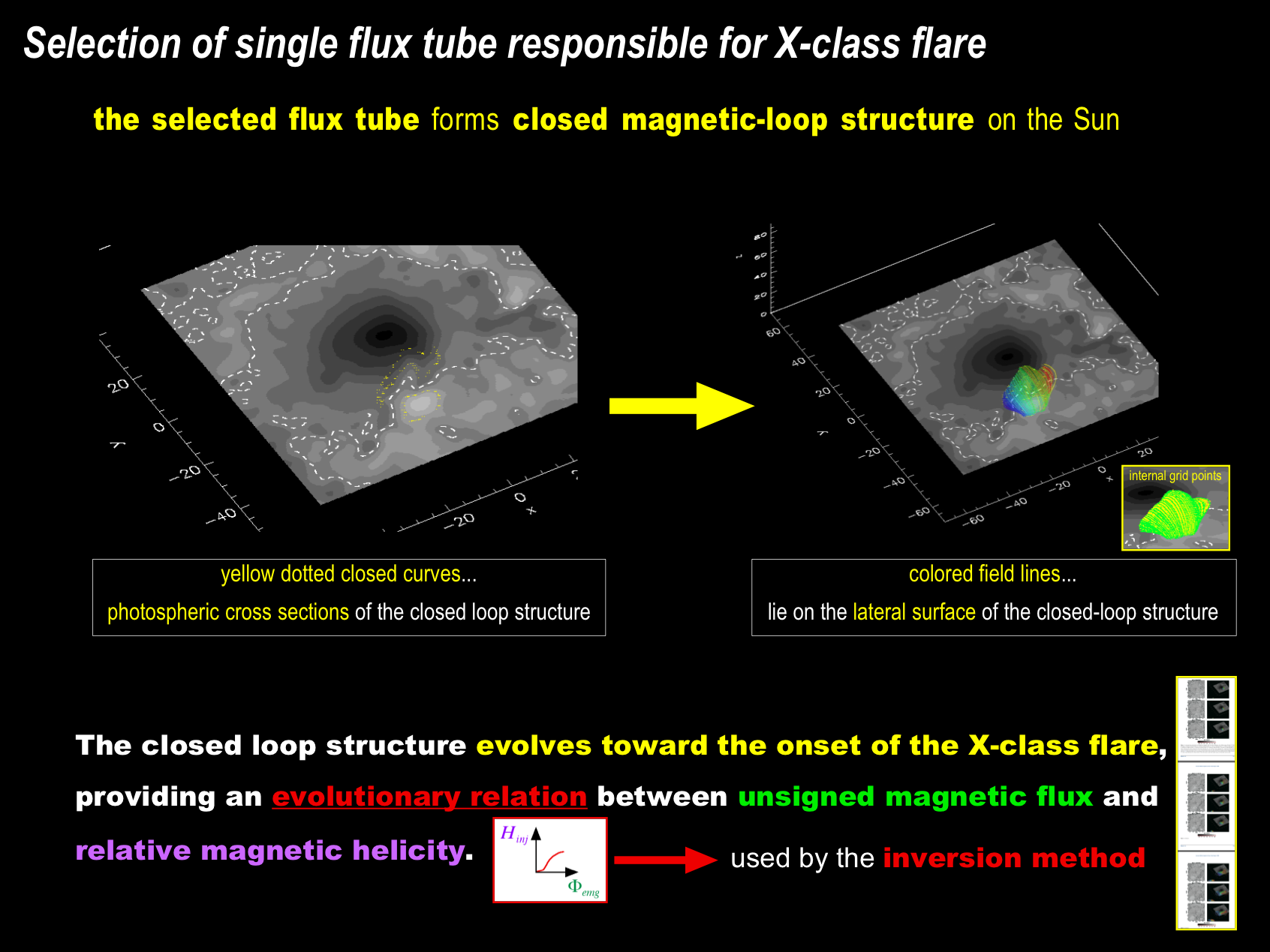
An issue is that while the inversion method can be applied to a single magnetic flux tube, multiple flux tubes may contribute to forming the magnetic structure of AR 10930 (Lim et al. 2010; Fan 2016; Magara 2019), so we have to select the single flux tube from among them that is responsible for the X-class flare observed in this AR. The selected flux tube forms closed magnetic-loop structure on the Sun, which evolves toward the onset of the flare. This evolving structure provides an evolutionary relation between unsigned magnetic flux and relative magnetic helicity (evolutionary path of the AR), which is used to solve the inverse problem via curve-fitting analysis.
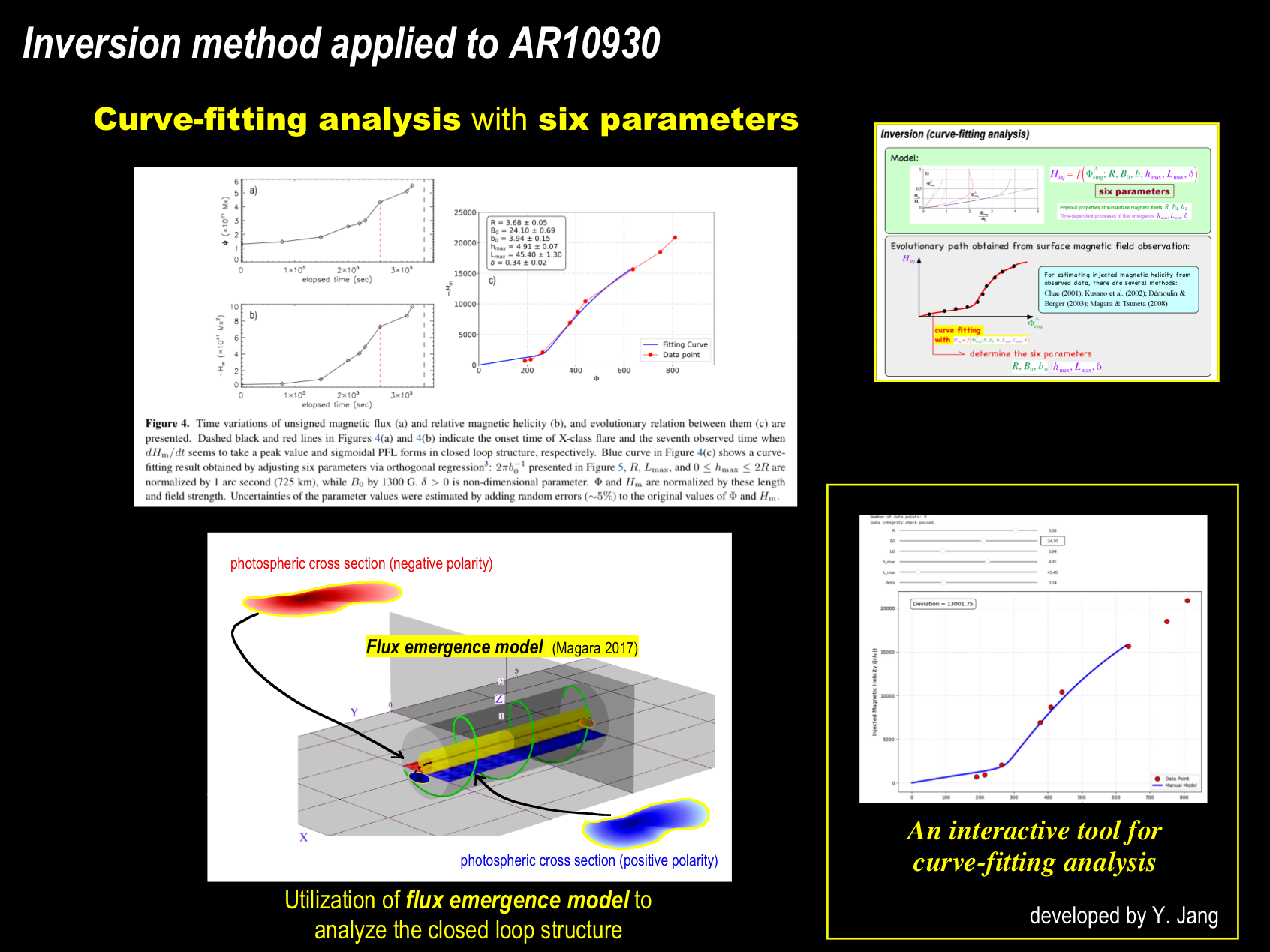
The relative magnetic helicity was obtained by first isolating the closed loop structure with Bff = 0 outside it and then using a formula presented in DeVore (2000).
By conducting the inversion method with the data points of Hm (Φ) in Figure 4c, we derived a fitting curve characterized by a forward S-shaped profile (Magara 2017) for the first seven data points. The deviation of the last two data points (eighth and ninth observed times) from this characteristic may suggest that by these times the closed loop structure had entered the phase of eruption that follows the formation of sigmoidal structure, as found in the spontaneous evolution of a subsurface field that emerges, structures itself, erupts, and finally produces a flare (Magara 2015).
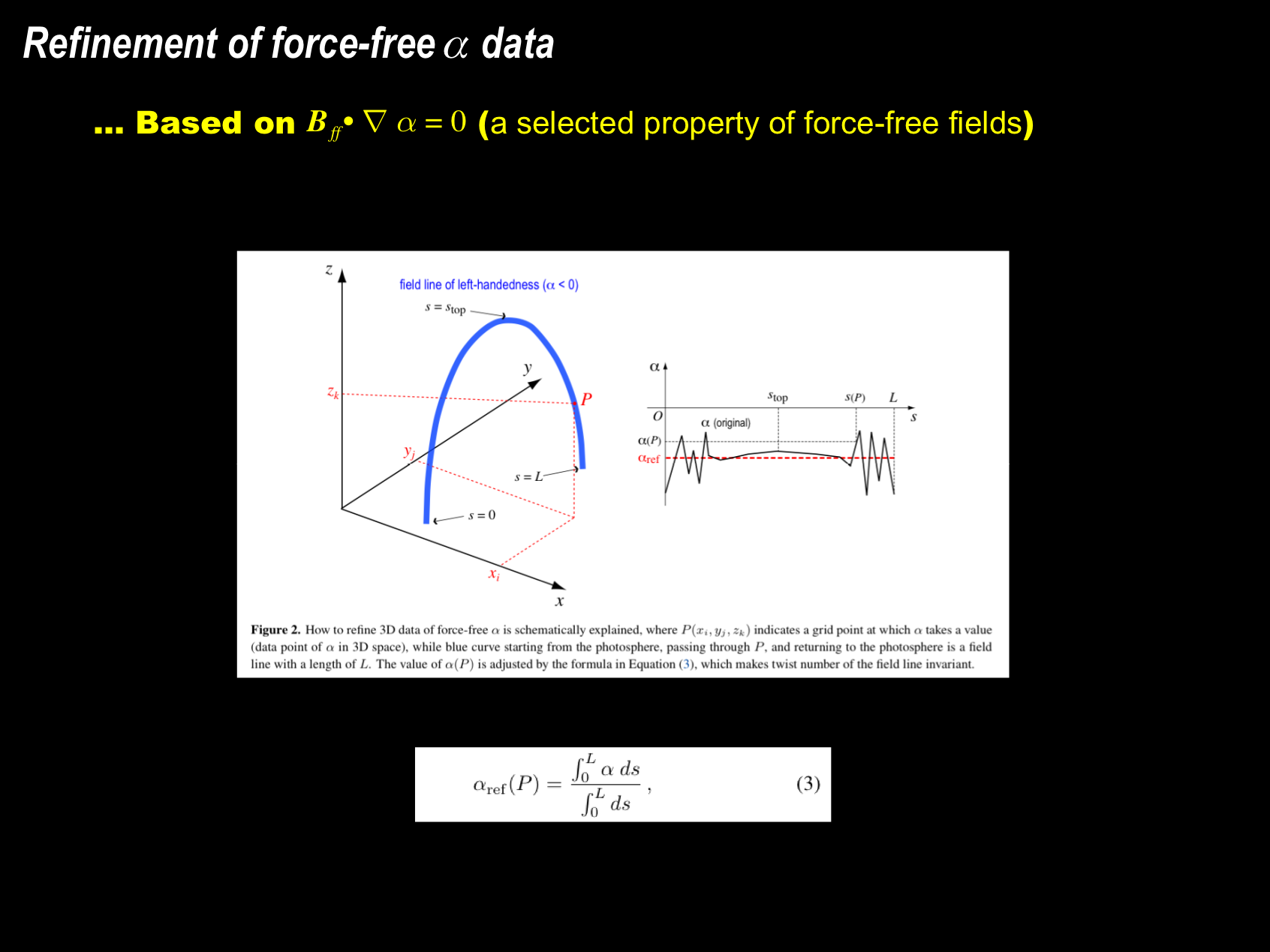
Any magnetic structure reconstructed using a force-free approximation from a photospheric field may somewhat deviate from a force-free state because the photospheric field is generally not in that state (Kang & Magara 2014; Wiegelmann & Sakurai 2021; Zhang & Zhang 2023). It may therefore be necessary to refine data obtained under that approximation on the basis of a selected property of force-free fields (Bff •∇α = 0). In principle, the formula in Equation (3) does not change the value of α (P) because α is constant along any force-free field line. On the other hand, the force-free α data is refined by that formula in which we take an average with the values of α measured in an upper atmospheric region where the force-free approximation tends to be more appropriate (Kang & Magara 2014).
(To refine force-free field data, we may have to adjust the direction and magnitude of current density j, the former of which could be done by reducing |j × B| toward zero, while the latter by a method such as that presented above in which the twist number of each field line is assumed to be invariant.)
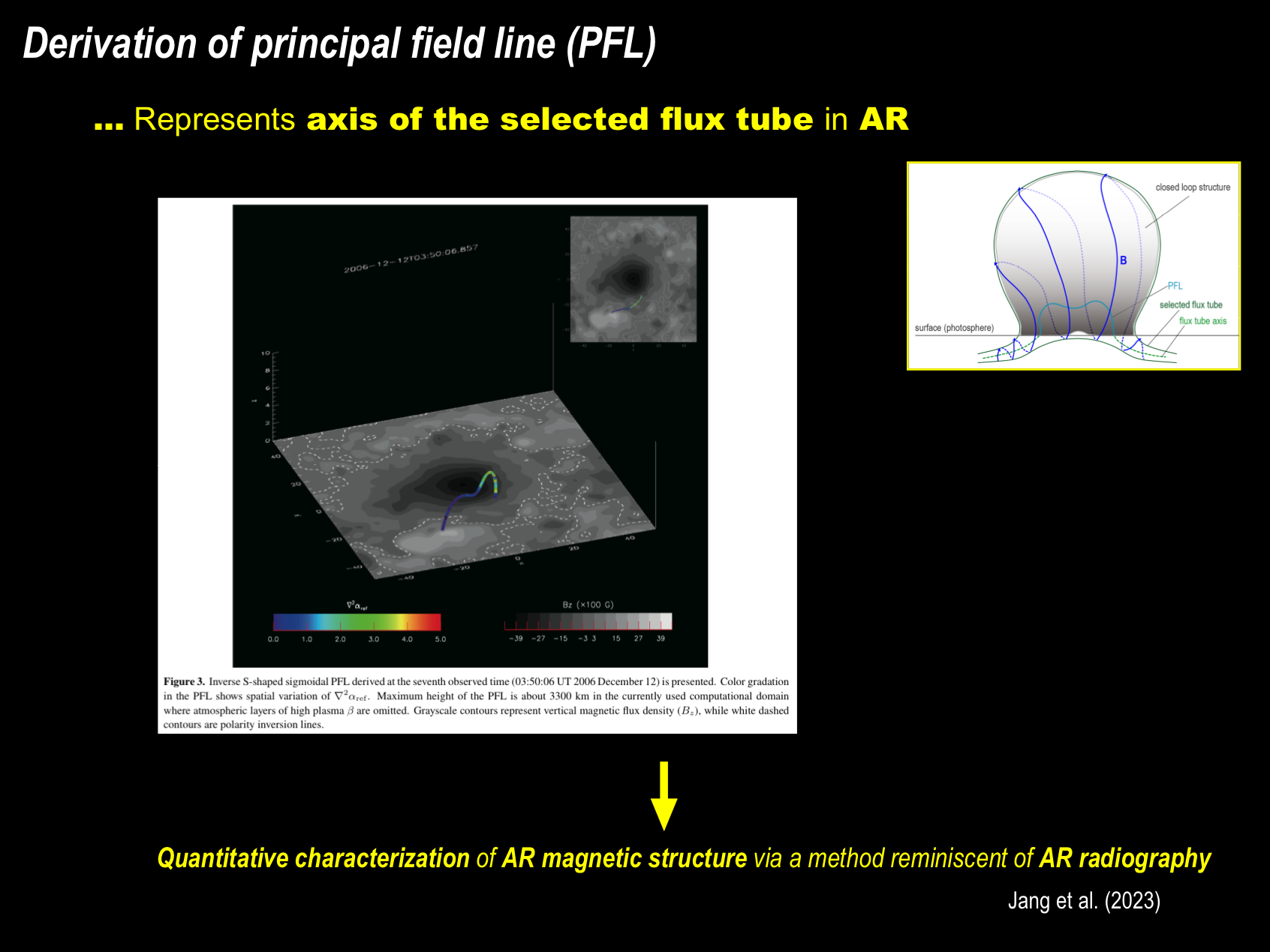
Figure 3 shows an inverse S-shaped sigmoidal PFL representing the axis of the selected flux tube in the AR, which was derived as a field line connecting locations with a local peak of αref (~ – 0.3) in the photosphere at the seventh observed time. This observed time belongs to Phase IV mentioned in Magara (2019) where the fragmentation of the positive sunspot and formation of inverse S-shaped sigmoidal structure observed in this phase were reproduced by simulating the emergence of a partially split flux tube. A high spatial concentration of αref (current density normalized by magnetic field strength) is found in part of the PFL where ∇2αref takes large positive values. The concept of PFL was introduced in Jang et al. (2023) to quantitatively characterize AR magnetic structure via a method reminiscent of AR radiography (ARR).
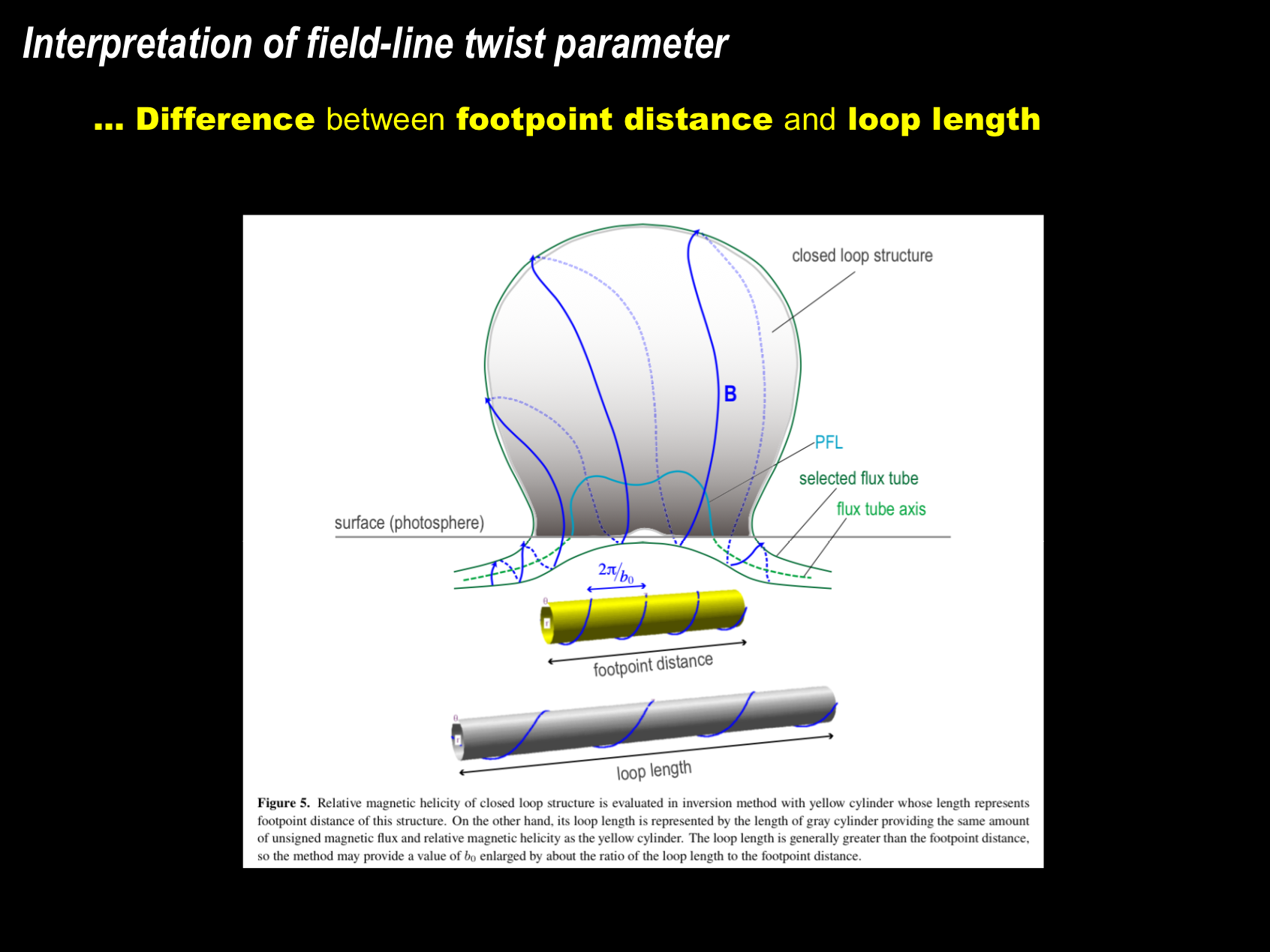
According to our previous work (Magara 2017), the parameter value of field-line twist seems several times larger than the expected one. A possible explanation of this discrepancy is presented in Figure 5, demonstrating that the relative magnetic helicity of the closed loop structure is evaluated in the method with the yellow cylinder whose length represents the footpoint distance of this structure. However, its loop length is generally greater than the footpoint distance, so the method may provide a value of b0 that is enlarged by about the ratio of the loop length to the footpoint distance.
- DeVore, C. R. 2000, Magnetic Helicity Generation by Solar
Differential Rotation, The Astrophysical Journal, 539,
944
- Fan, Y. 2016, Modeling the Initiation of the 2006 December
13 Coronal Mass Ejection in AR 10930: The Structure
and Dynamics of the Erupting Flux Rope, Astrophysical
Journal, 824, 93
- Jang, Y., Yi, S., Magara, T. 2023, Magnetic configuration related to the coronal heating and solar wind generation.
II. Quantitative characterization of active-region
magnetic structure based on the geometric property of
force-free α, Publications of the Astronomical Society of
Japan, 75, 787
- Kang, J. & Magara, T. 2014, Investigation of force-freeness of
a solar emerging magnetic field via application of the virial
theorem to magnetohydrodynamic simulations, Publications
of the Astronomical Society of Japan, 66, 121
- Lim, E., et al. 2010, The Formation of a Magnetic Channel
by the Emergence of Current-Carrying Magnetic Fields,
The Astrophysical Journal, 719, 403
- Magara, T. 2015, MHD simulation for investigating the evolutionary
path of a solar magnetic field that emerges,
structures itself, erupts, and produces a
flare, Publications
of the Astronomical Society of Japan, 67, L6
- Magara, T.. 2017, An Inversion Method for Deriving Physical
Properties of a Subsurface Magnetic Field from Surface
Magnetic Field Evolution. I. Application to Simulated
Data, Journal of the Korean Astronomical Society,
50, 179
- Magara, T.. 2019, Merging and Fragmentation in the Solar
Active Region 10930 Caused by an Emerging Magnetic
Flux Tube with Asymmetric Field-Line Twist Distribution
along Its Axis, Journal of the Korean Astronomical
Society, 52, 89
- Wiegelmann, T., Sakurai, T. 2021, Solar force-free magnetic field, Living Reviews in Solar Physics, 18, 1
- Yi, S., Choe, G. S., Cho, K.-S., Solanki, S. K., Büchner,
J. 2022, Reconstruction of Coronal Magnetic Fields Using
a Poloidal-Toroidal Representation, The Astrophysical
Journal, 937, 11
- Zhang, M., Zhang, H. 2023, The Force-freeness of the Solar
Photosphere: Revisit with New Approach and Large Data
Sets, The Astrophysical Journal Letters, 956, L17








